Spike discharge prediction based on neuro-fuzzy system
Abstract
This paper presents the development and evaluation of different versions of neuro-fuzzy model for prediction of spike discharge patterns. The author aims to predict the spike discharge variation using first spike latency and frequency-following interval. In order to study the spike discharge dynamics, the author analyzed the cerebral cortex data of the cat. Adaptive neuro-fuzzy inference systems (ANFIS), Wang and Mendel, dynamic evolving neural-fuzzy inference system, hybrid neural fuzzy inference system, genetic for lateral tuning and rule selection of linguistic fuzzy system (GFS.LT.RS) and subtractive clustering and fuzzy c-means algorithms are applied for data. Among these algorithms, ANFIS and GFS.LT.RS models have better performance. On the other hand, ANFIS and GFS.LT.RS algorithms can be used to predict the spike discharge dynamics as a function of first spike latency and frequency with a higher accuracy compared to other algorithms.
Keywords
Introduction
Recording action potentials (spikes) from the neural cells makes it possible to investigate their health, stability, and sensitivity[1]. Different characteristics of the electrical activity of neurons can be considered in the study of neural coding. One important concept in this area is spike discharge that is a type of transient waveforms present in the brain activity and includes a high correlation with seizure occurrence[2].
Studies on movement indole illustrated that this process is related to the neuronal discharge[3,4]. For example, the study on activity of arm-related neurons and their relationship between premotor cortical cell activity and direction of arm movement shows that the cells activity varies in an orderly fashion with the direction of movement[5]. Also, detection of spike discharge in the electroencephalogram is an important way of diagnosis of the disease[2]. Different algorithms like neural networks, logistic regression, and neuro-fuzzy model can be applied for detection of epileptic seizure[2,6,7]. There are many similarities between human and animal brain’s neural coding and many studies used animal modeling for investigation the spike discharge[8-11]. Johnsen and Levine[1] analyzed 26 pairs of units recorded from twenty-four retinal ganglion cells in the isolated goldfish retina and examined the cross-correlation histogram for the maintained discharge of each pair of cells. Their results showed that it is unlikely that differences in latency could be attributed to the unequal effectiveness of the stimuli for the 2 units. Batuev et al.[12] investigated the postsynaptic response of motor cortex neurons of the cat in response to the stimulation of different modalities and showed that it responds with a wide range of peripheral inputs. The electrical changes in the cerebral cortex can correspond with the electric changes in muscle and nerve[13]. The studies of the functional organization of the motor cortex show that this cortical area is composed of modules consisting of columnar aggregates of neurons related to different aspects of the same movement[14]. The current-flow and current-source-density analysis of the direct cortical response in the somatosensory cortex of rats show that the activation and magnitude of direct cortical response depend on stimulus strength and frequency[15].
In this paper, the variation of spike discharge as a function of first spike latency and the frequency-following interval is analyzed. First spike latency is the time delay between stimulus onset and first action potential[16]. Neuro-fuzzy model is a combination of artificial neural network and fuzzy logic approaches. It is a powerful tool for dealing with uncertainty and widely used for analyzing electrical activity of neurons. It is widely used for analyzing the electrical activity of the neurons[17-20]. The adaptive neuro-fuzzy inference systems (ANFIS) method was successfully applied for electroencephalography signals with a high accuracy of the results obtained[17]. A feature extraction method through the time-series prediction based on ANFIS model for brain-computer interface applications has been proposed by Hsu[18]. In this model, ANFISs is used for prediction of time-series for the left and right motor imagery classification, respectively. It is shown that neuro-fuzzy is an accurate model diagnosing epilepsy[20].
Different versions of the neuro-fuzzy model have been used to find the model with higher accuracy. In all models, the spike discharge is considered as an output of the model, while first spike latency and spike frequency are considered as inputs. Using neuro-fuzzy model as a predictor of spike discharge, we are able to use insufficient crisp inputs to make an accurate decision about spike discharge. We used first spike latency and frequency-following interval in the input layer of the neuro-fuzzy system and output was the spike discharge. The structure of this paper is as follows.
First, we discuss spike discharge, latency, and frequency. Section 2 provides a brief description of ANFIS, Wang and Mendel (WM), dynamic evolving neural-fuzzy inference system (DENFIS), hybrid neural fuzzy inference system (HyFIS) and subtractive clustering and fuzzy c-means (SBC) algorithms and section 3 presents the performance of different neuro-fuzzy algorithms for analysis of cat data.
Neuro-fuzzy model
Neuro-fuzzy model is a combination of artificial neural networks and fuzzy logic and it uses capabilities of both models. It applies a neural networks structure and at the same time uses if-then rules in fuzzy systems. It uses prior knowledge to compute membership function and different learning algorithms of neural networks, including the back-propagation algorithm[21].
The different types of neuro-fuzzy systems used in this paper are as follow: ANFIS, WM, DENFIS, HyFIS[22], genetic for lateral tuning and rule selection of linguistic fuzzy system (GFS.LT.RS)[23], SBC[24,25]. Here we provide a short description each of them.
ANFIS
ANFIS model is a well-known neuro-fuzzy system that implements a Sugeno fuzzy system and uses a t-norm and differentiable membership function[26,27]. For a system with two rules, we can build the following neuro-fuzzy structure.
For given two inputs x0 and y0 and corresponding linguistic labels Ai and Bi, each neuron in the first layer of neuro-fuzzy model transmit the crisp signal to the next layer (Algorithm 1).
Algorithm 1: ANFIS model
This algorithm has two main stages, the forward and backward steps. The forward step has five layers as follows: (1) first layer maps the crisp inputs using bell-shaped membership function as follows: Ai (u) = exp{-1/2 [(u - ai1)/(bi1)]2} and Bi(u) = exp{-1/2 [(u - ai2)/bi2)]2}, where {ai1, ai2, bi1, bi2} is the parameters set. These parameters are tuned using the specified input/output training data (first spike latency and frequency-following interval/spike discharge variation); (2) the second layer is responsible for fuzzification and each neuron in this layer determines the fuzzy degree received crisp input: α1 = A1 (x0) × B1 (y0) = A1 (x0) ^ B1 (y0) and α2 = A2 (x0) × B2 (y0) = A2 (x0) ^ B2 (y0); (3) neurons in the third layer correspond to fuzzy rules and receive inputs from fuzzification neurons in the second layer. The outputs of layer 3 are as follow: β1 = α1/(α1 + α2) and β2 = α2/(α1 + α2); (4) layer 4 or output membership layer combine all its inputs by using the fuzzy operation union: β1z1 = β1 (α1x0 + b1y0) and β2z2 = β2 (α2x0 + b2y0); and (5) the last layer is responsible for Defuzzification: o = β1z1 + β2z2. In the backward process, the errors are propagated backward and the parameters are updated by gradient descent technique.
WM
WM model is another type of neuro-fuzzy system that developed by Wang and Mendel[28] that has high performance for regression tasks. First, it divides input and outputs into the fuzzy region and assigns a membership function to each region. Then finds a rule for each pair of input data. In the next step, a degree is assigned to each rule. After assigning degrees, they are combined. The final rule is obtained after deleting redundant rules. Algorithm 2 provides more details about WM algorithm.
Algorithm 2: WM model
Division numerical input and output data spaces into fuzzy regions generate fuzzy IF-THEN rules covering the training data determining a degree for each rule. Eliminating redundant rules and obtaining a final rule base. More details about the algorithm is as follows[28]: (1) for each example ep = (ap1 ,…,apm, y), p = 1, 2,.., m where y is class value, builds fuzzy rule with the highest compatibility value; (2) calculate the importance degree for each of the generated rule. If "Rk: IF X1 is A1 AND...AND Xm is Am, Then Y is B", is the rule for ep, then the importance degree of this rule is: G(Rk) = t [A(ap1),…, A(apm), B(y)], where t is a t-norm, A(api) represents the membership degree of api and B(y) is the membership degree for the fuzzy set with the highest membership degree; (3) eliminate redundant rules, from the set of rules; (4) eliminate conflicting rules. If two or more rules of the remaining set have equal antecedents, discard the rule with the smallest importance degree; and (5) compose the final rule base using the remaining rules.
DENFIS
DENFIS is another fuzzy inference system that developed by Kasabov and Song[29]. The output of the system is based on m-most activated fuzzy rules and evolving clustering method is applied to determine the cluster center (Algorithm 3).
Algorithm 3: DENFIS model
(1) Choose cluster center from training data; (2) determine the cluster centers using the evolving clustering method partition the input space and to find optimal parameters on the consequent part; and (3) update the parameters on the consequent part. All fuzzy membership functions are triangular type functions which depend on three parameters as given by the following equation[30]:
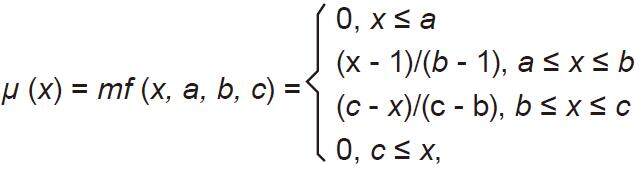
where b is the value of the cluster center on the x dimension.
HyFIS
HyFIS has two general steps for learning[22]. In the first step, the Wang and Mendel is used for knowledge acquisition. In the second step, the input vector is propagated forward in the network and parameter updating is performed using backpropagating the error using a gradient descending approach[30].
Algorithm 4: HyFIS model
(1) Uses the techniques of Wang and Mendel to acquire the knowledge; and (2) use gradient descent-based to learn parameters of the structure. The training parameters are the centers and the widths of the Gaussian membership functions present in layers 2 and 4 defined by the following equation[30]:
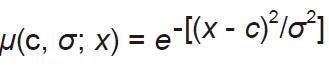
where c is the centre of the function and σ is the width of the function.
GFS.LT.RS
GFS.LT.RS is proposed by Alcalá et al.[23] that performs an evolutionary lateral tuning of membership functions in constructing FRBS model to obtain higher accurate linguistic models (Algorithm 5).
Algorithm 5: GFS.LT.RS model
GFS.LT.RS uses the Wang and Mendel to construct the population, evaluate the chromosome using mean square error, and minimize the number of rules.
SBC
SBC[25,31] is checking each data point's distance from all other data points to find the cluster centers. More details about SBC algorithm is provided in the Algorithm 6.
Algorithm 6: SBC model
Use subtractive clustering method to obtain the cluster centeres (generating the rules): (1) choose the highest potential as the cluster center. Here a density measure at data point ra is defined as:
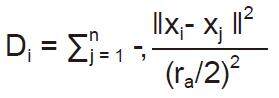
where ra is a positive constant. The data points outside neighborhood that defined by ra contribute only slightly to the density measure. The data point with the highest density measure is selected as the first cluster center; (2) update the potential of each data point. Let xcl be the point selected and Dcl its density measure. The density measure for each data point xi is revised by the formula:
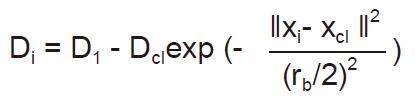
where rb is a positive constant. The data points near the first cluster center xcl have density measures and making the points unlikely to be selected as the next cluster center; and (3) optimize the cluster centers using fuzzy c-means.
Results
To verify the effectiveness of the neuro-fuzzy algorithms we carried out a number of numerical experiments with the cortex of the somatosensory/motor system of the Cat data set on a PC with Processor Intel(R) Core(TM) i5-3470S CPU 2.90 GHz and 8 GB RAM running under Windows XP. The cortex of the somatosensory/motor system of the Cat data[32] was used in this paper. This data is based on recording neurons of extracellularly in post cruciate cerebral cortex of cats. It is neuronal responsiveness of each of the four paws to strong cortical surface stimulation to understand facilitatory and inhibitory modulation of wide-field neurons by small-field neurons. Two groups of data from the cerebral cortex of the cat data sets are considered for evaluation of the algorithms: Contralateral Forepaw (CF) Cortex (Chloralose) and Contralateral Hindpaw (CH) Cortex (Chloralose). The Contralateral Forepaw (CF) Cortex (Chloralose) is based on the measurements of 4,272 neurons, but Contralateral Hindpaw (CH) Cortex (Chloralose) contains data of 991 neurons. Various versions of neuro-fuzzy algorithms from R package are used to evaluate the algorithms’ error for each data. The R Project for Statistical Computing is an environment for statistical computing and graphics that contains comprehensive libraries of machine learning and statistical analysis applications that are available on[33].
Results of Forepaw (CF) Cortex (Chloralose) analysis
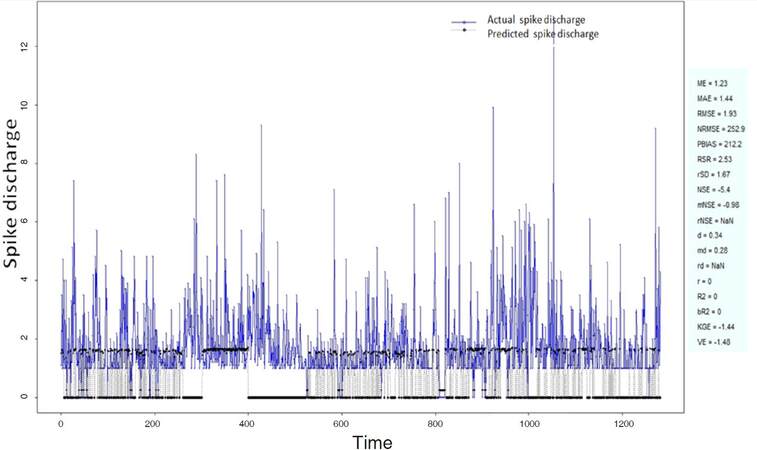
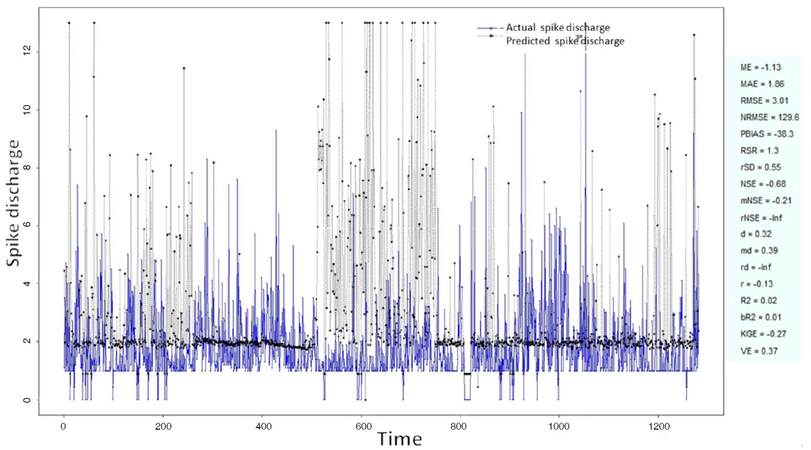
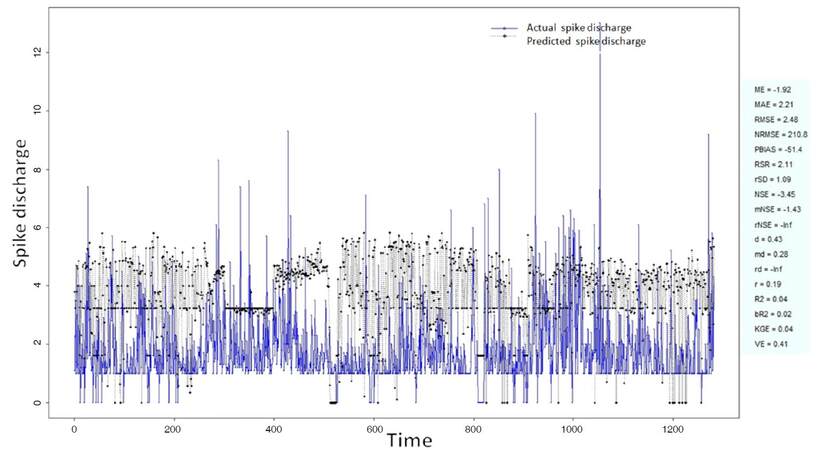
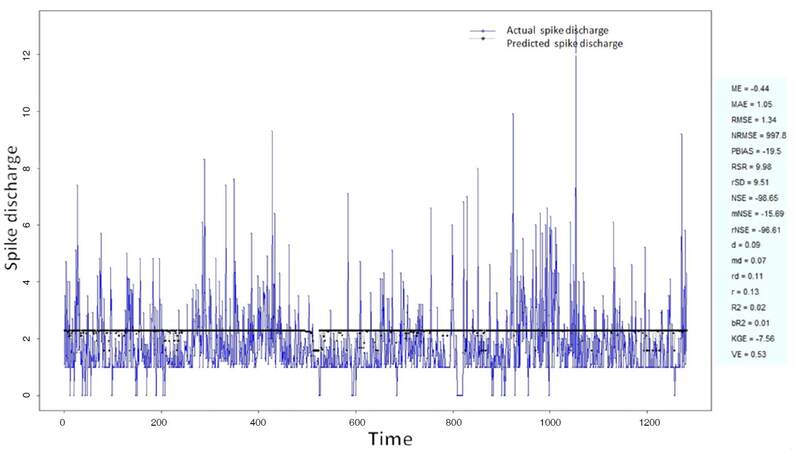
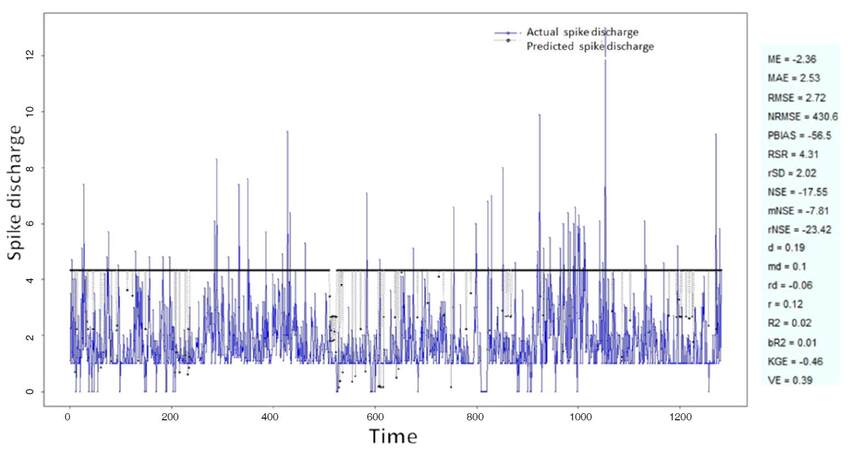
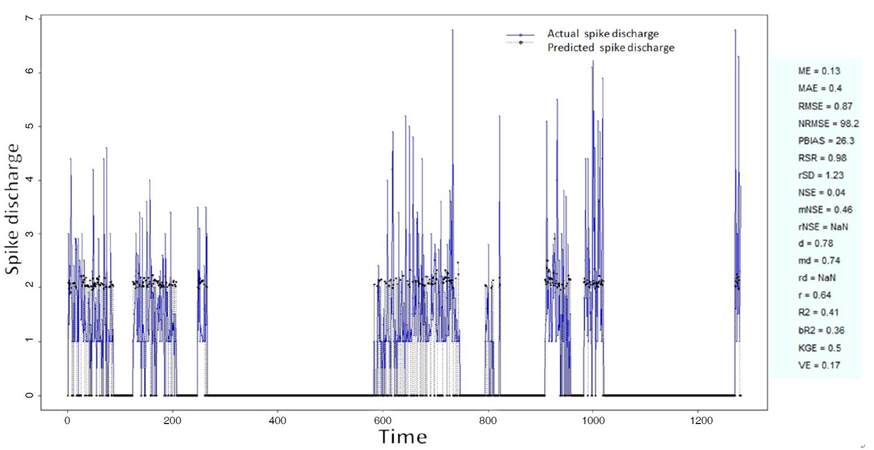
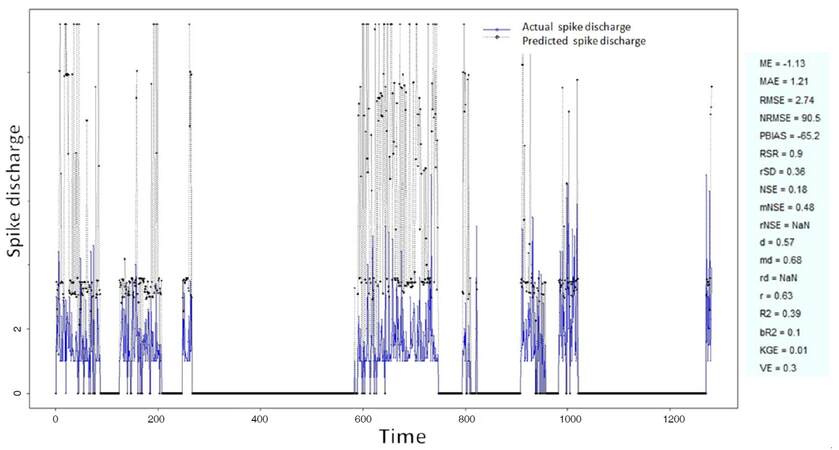
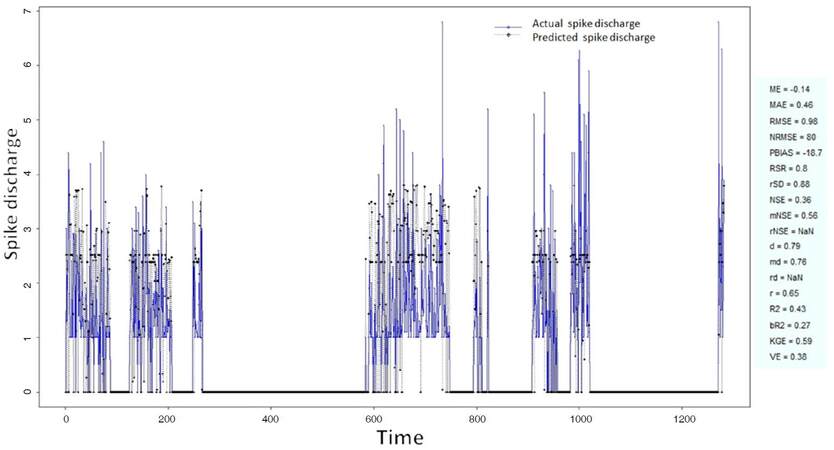
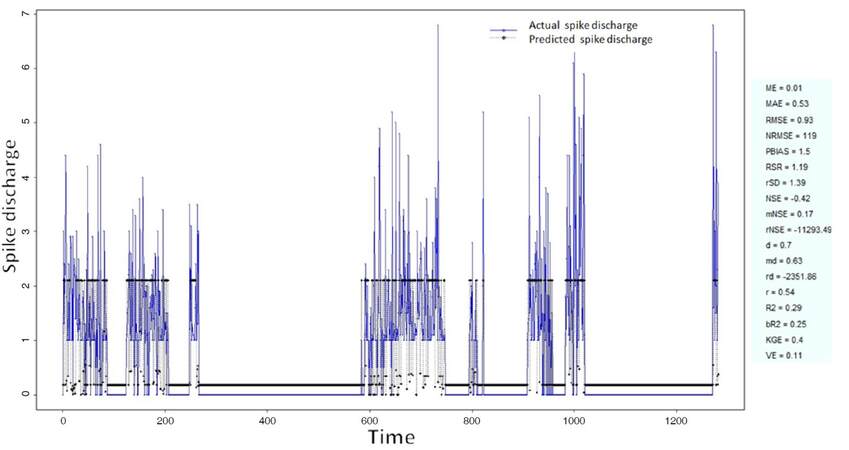
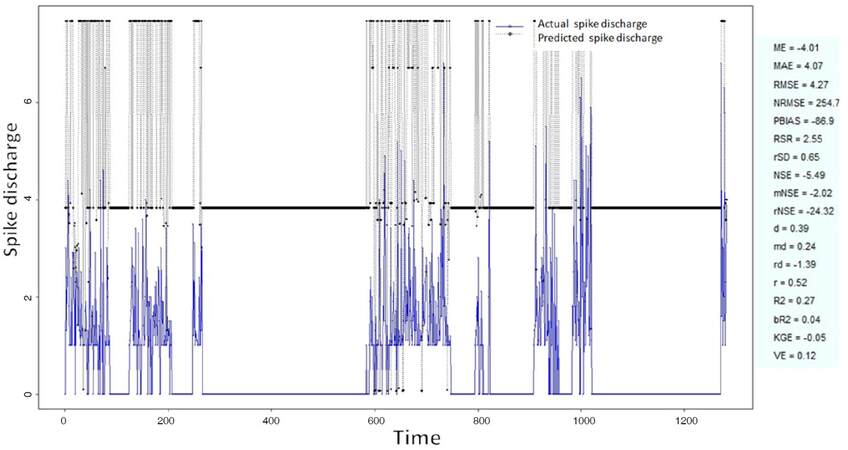
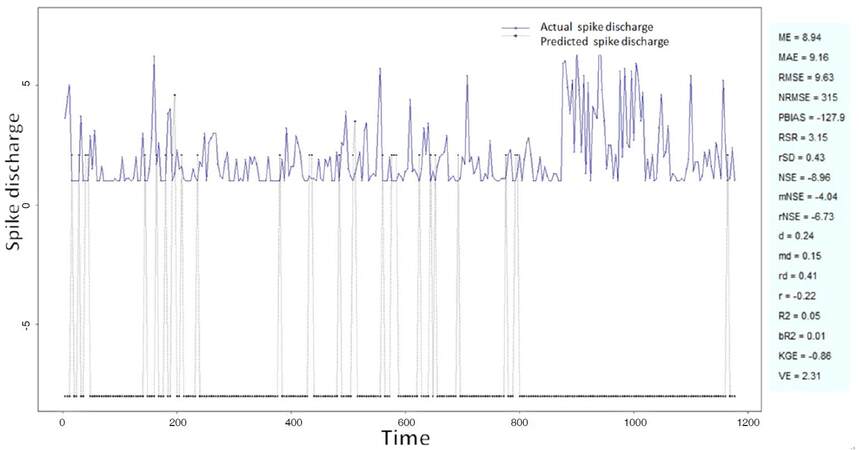
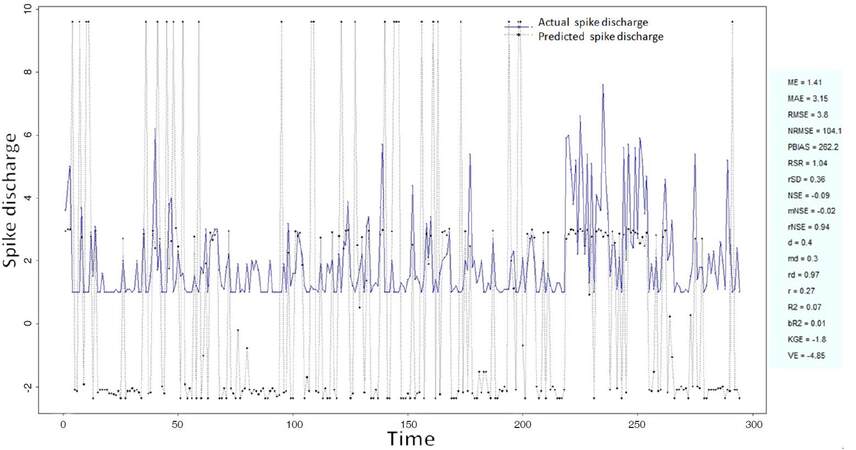
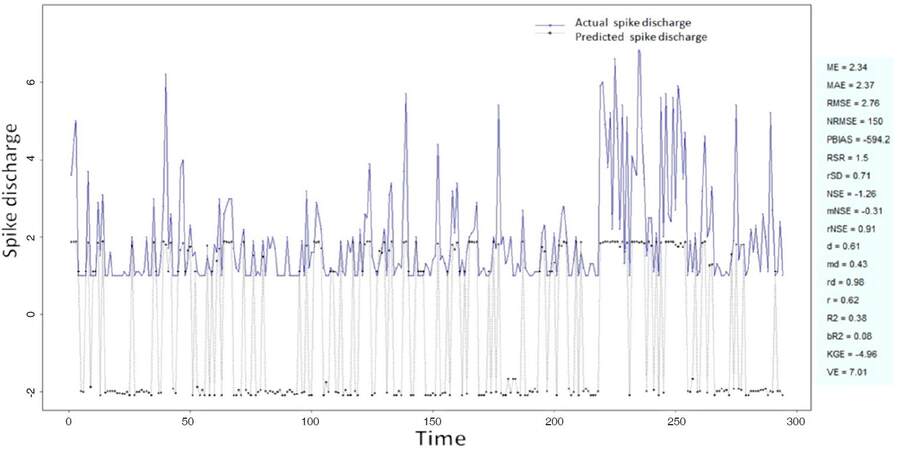
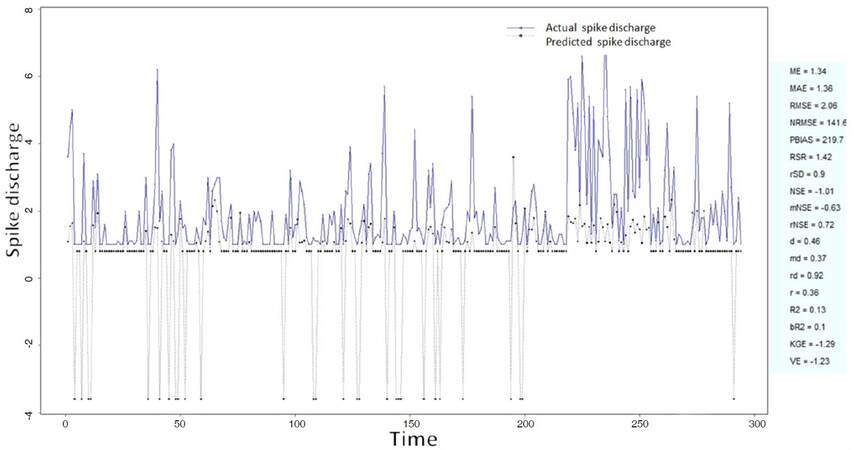
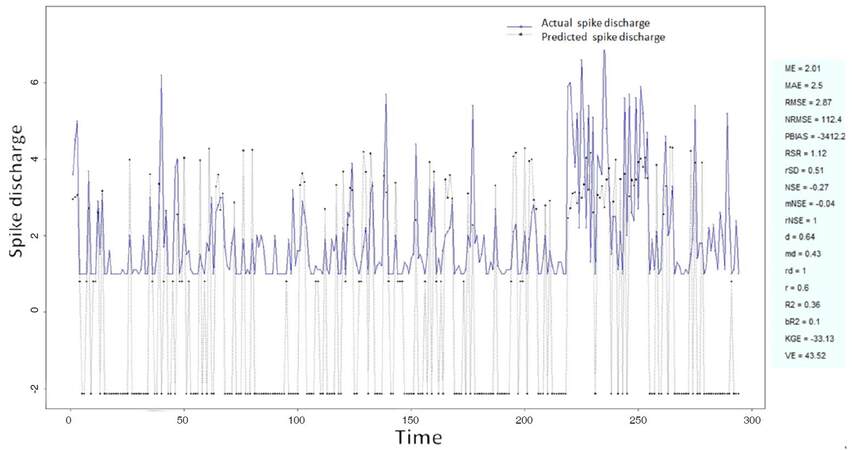
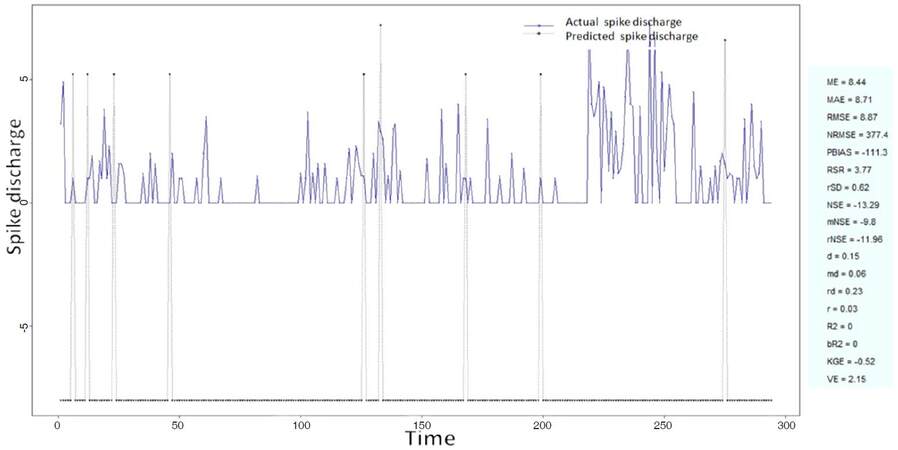
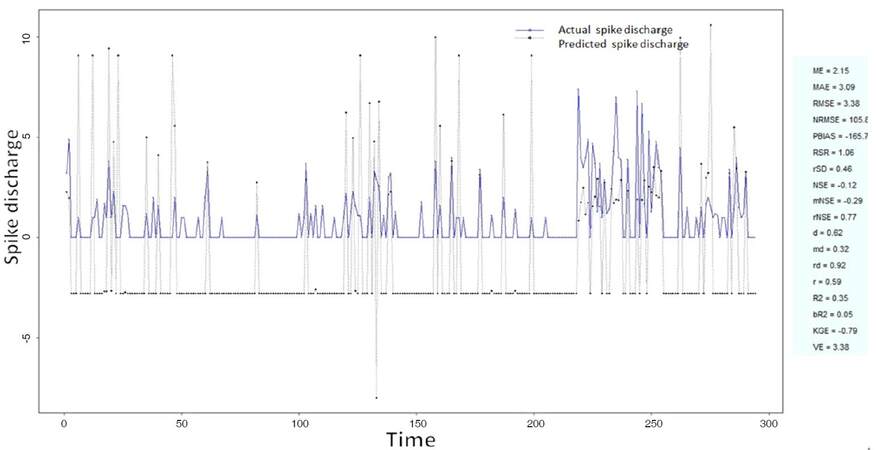
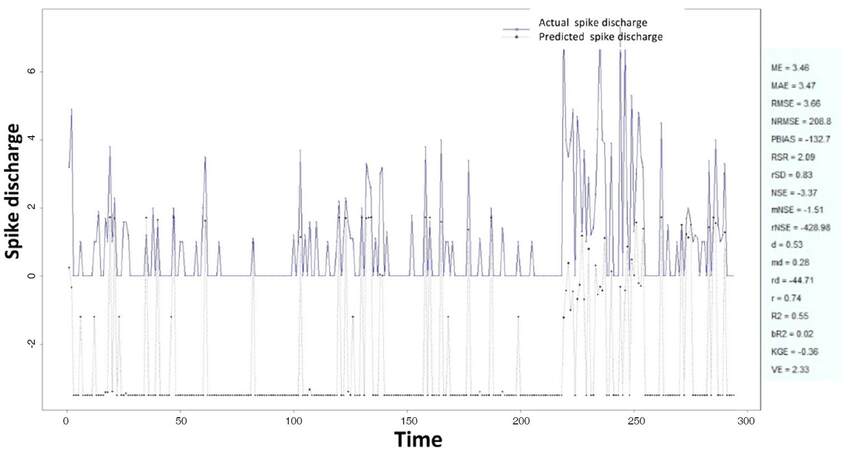
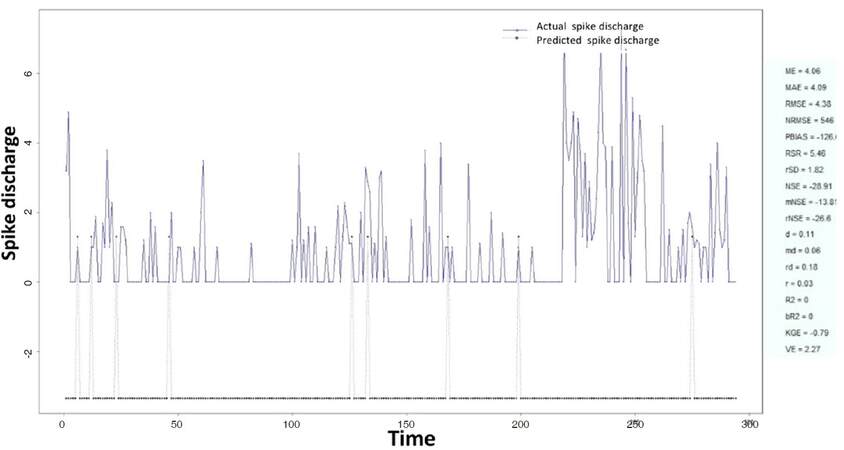
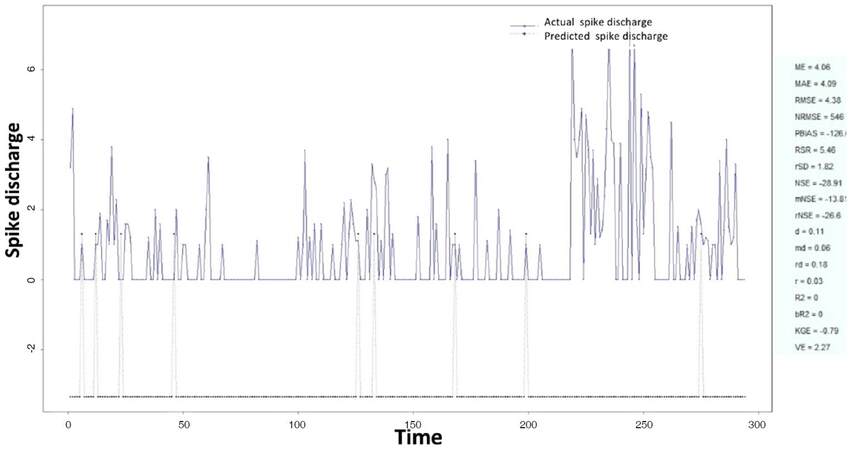
The Ipsilateral and Contralateral data from Forepaw Cortex data are considered for analysis. The results of application of neuro-fuzzy algorithm to the Ipsilateral Forepaw Cortex data are presented in Figures 1-5. The first spike latency and ipsilateral forepaw frequency following interval (msec) are used as inputs, while mean spikes per discharge is used as output of the model. Figures 1-20 contains the actual spikes per discharge value that is computed using neuro-fuzzy algorithm. Also, some statistics about the analysis is illustrated in Figures 1-20. The results show that the smallest Root Mean Square Error (RMSE) is obtained by HYFIS algorithm (RMSE = 1.34) and the biggest RMSE is obtained by WM model (RMSE = 2.72). Figures 6-15 present the results of application for neuro-fuzzy algorithm for the Contralateral Forepaw Cortex data. Again the 1st spike latency and ipsilateral forepaw frequency following interval (msec) are used as inputs and mean spikes per discharge is used as output of the model. The results demonstrate that the smallest Root Mean Square Error (RMSE) is obtained using HYFIS algorithm (RMSE = 0.93) and the biggest RMSE is obtained by WM model (RMSE = 4.27).
Figure 1. Spike discharge prediction for cat ipsilateral forepaw cortex using adaptive neuro-fuzzy inference systems algorithm
Figure 3. Spike discharge prediction for cat ipsilateral forepaw cortex using genetic for lateral tuning and rule selection of linguistic fuzzy system algorithm
Figure 4. Spike discharge prediction for cat ipsilateral forepaw cortex using Hybrid neural Fuzzy Inference System algorithm
Figure 5. Spike discharge prediction for cat ipsilateral forepaw cortex using Wang and Mendel algorithm
Figure 6. Spike discharge prediction for cat contralateral forepaw cortex using adaptive neuro-fuzzy inference systems algorithm
Figure 8. Spike discharge prediction for cat contralateral forepaw cortex using genetic for lateral tuning and rule selection of linguistic fuzzy system algorithm
Figure 10. Spike discharge prediction for cat contralateral forepaw cortex using Wang and Mendel algorithm
Figure 11. Spike discharge prediction for cat contralateral hindpaw cortex using adaptive neuro-fuzzy inference systems algorithm
Figure 13. Spike discharge prediction for cat contralateral hindpaw cortex using subtractive clustering and fuzzy c-means algorithm
Figure 14. Spike discharge prediction for cat contralateral hindpaw cortex using genetic for lateral tuning and rule selection of linguistic fuzzy system algorithm
Figure 15. Spike discharge prediction for cat contralateral hindpaw cortex using Wang and Mendel algorithm
Figure 16. Spike discharge prediction for cat ipsilateral hindpaw cortex using adaptive neuro-fuzzy inference systems algorithm
Figure 18. Spike discharge prediction for cat ipsilateral hindpaw cortex using subtractive clustering and fuzzy c-means algorithm
Figure 19. Spike discharge prediction for cat ipsilateral hindpaw cortex using genetic for lateral tuning and rule selection of linguistic fuzzy system algorithm
Results of Hindpaw Cortex (Chloralose) data analysis
The Hindpaw Cortex is divided into two parts: the Contralateral Forepaw Cortex and Ipsilateral Hindpaw Cortex. Then different neuro-fuzzy algorithms have been applied to them. The best RMSE is obtained using GFS LT RS (RMSE = 2.06), the smallest Root Mean Square Error (RMSE) is obtained using HYFIS algorithm (RMSE = 0.93), and the biggest RMSE is btained by WM model (RMSE = 4.27). The WM algorithm provides better accuracy compared with other algorithm (RMSE = 2.73).
Conclusion
In this section we presented the development and evaluation of different versions of adaptive neuro-fuzzy model including ANFIS, WM, DENFIS, HyFIS, GFS.LT.RS and SBC algorithms for prediction of spike discharge. Results reveal that spike discharge can be predicted using the neuro-fuzzy model where first spike latency and frequency-following interval are the inputs and spike discharge is the output of the model.
Declarations
Authors’ contributionsThe author contributed solely to the paper.
Financial support and sponsorshipNone.
Conflicts of interestThe author certifies that he has no affiliations with or involvement in any organization or entity with any financial or non-financial interest in the subject matter or materials discussed in this manuscript.
Patient consentNot applicable.
Ethics approvalNot applicable.
Copyright© The Author(s) 2017.
REFERENCES
1. Johnsen JA, Levine MW. Correlation of activity in neighbouring goldfish ganglion cells: relationship between latency and lag. J Physiol 1983;345:439-49.
2. Subasi A. Automatic detection of epileptic seizure using dynamic fuzzy neural networks. Exp Syst Appl 2006;31:320-8.
3. Kalaska JF. What parameters of reaching are encoded by discharges of cortical cells. In: Humphrey DR, Freund JH, editors. Motor control: Concepts and Issues. Chichester: Wiley; 1991. pp. 307-30.
4. Fu QG, Flament D, Coltz JD, Ebner TJ. Relationship of cerebellar Purkinje cell simple spike discharge to movement kinematics in the monkey. J Neurophysiol 1997;78:478-91.
5. Caminiti R, Johnson PB, Galli C, Ferraina S, Burnod Y. Making arm movements within different parts of space: the premotor and motor cortical representation of a coordinate system for reaching to visual targets. J Neurosci 1991;11:1182-97.
6. Pang CC, Upton AR, Shine G, Kamath MV. A comparison of algorithms for detection of spikes in the electroencephalogram. IEEE Trans Biomed Eng 2003;50:521-6.
7. Subasi A, Erçelebi E. Classification of EEG signals using neural network and logistic regression. Comput Methods Programs Biomed 2005;78:87-99.
8. Fisher RS, Prince DA. Spike-wave rhythms in cat cortex induced by parenteral penicillin. II. Cellular features. Electroencephalogr Clin Neurophysiol 1977;42:625-39.
9. Marino J, Canedo A, Aguilar J. Sensorimotor cortical influences on cuneate nucleus rhythmic activity in the anesthetized cat. Neuroscience 2000;95:657-73.
10. Sitnikova E. Thalamo-cortical mechanisms of sleep spindles and spike-wave discharges in rat model of absence epilepsy (a review). Epilepsy Res 2010;89:17-26.
11. Cavelier P, Bossu JL. Dendritic low-threshold Ca2+ channels in rat cerebellar Purkinje cells: possible physiological implications. Cerebellum 2003;2:196-205.
12. Batuev AS, Lenkov DN, Pirogov AA. Postsynaptic responses of motor cortex neurons of cats to sensory stimulation of different modalities. Acta Neurobiol Exp (Wars) 1974;34:317-21.
15. Harding GW. The currents that flow in the somatosensory cortex during the direct cortical response. Exp Brain Res 1992;90:29-39.
16. Gollisch T, Meister M. Rapid neural coding in the retina with relative spike latencies. Science 2008;319:1108-11.
17. Güler I, Ubeyli ED. Adaptive neuro-fuzzy inference system for classification of EEG signals using wavelet coefficients. J Neurosci Methods 2005;148:113-21.
18. Hsu WY. EEG-based motor imagery classification using neuro-fuzzy prediction and wavelet fractal features. J Neurosci Methods 2010;189:295-302.
19. Pohl V, Fahr E. Neuro-fuzzy recognition of K-complexes in sleep EEG signals. Eng Med Biol Soc 1995;1:789-90.
20. Subasi A. Application of adaptive neuro-fuzzy inference system for epileptic seizure detection using wavelet feature extraction. Comput Biol Med 2007;37:227-44.
21. Tsoukalas LH, Uhrig RE. Fuzzy and neural approaches in engineering. New York: John Wiley & Sons, Inc; 1996.
22. Kim J, Kasabov N. HyFIS: adaptive neuro-fuzzy inference systems and their application to nonlinear dynamical systems. Neural Netw 1999;12:1301-19.
23. Alcalá R, Alcalá-Fdez J, Herrera F. A proposal for the genetic lateral tuning of linguistic fuzzy systems and its interaction with rule selection. IEEE Transact Fuzzy Syst 2007;4:616-35.
24. Yager RR, Filev DP. Generation of fuzzy rules by mountain clustering. J Intell Fuzzy Syst 1994;2:209-19.
25. Chiu S. Method and software for extracting fuzzy classification rules by subtractive clustering. In: Fuzzy Information Processing Society. NAFIPS: Biennial Conference of the North American; 1996. pp. 461-5.
26. Jang JSR. ANFIS: adaptive-network-based fuzzy inference system. IEEE Transact Syst Man Cybernet 1993;3:665-85.
27. Takagi T, Sugeno M. Fuzzy identification of systems and its applications to modeling and control. IEEE Transact Syst Man Cybernet 1985;SMC-15:116-32.
28. Wang LX, Mendel JM. Generating fuzzy rules by learning from examples. IEEE Transact Syst Man Cybernet 1992;22:1414-27.
29. Kasabov NK, Song Q. DENFIS: dynamic evolving neural-fuzzy inference system and its application for time-series prediction. IEEE Transact Fuzzy Syst 2002;2:144-54.
30. Tung SW, Quek C, Guan C. T2-HyFIS-yager: type 2 hybrid neural fuzzy inference system realizing yager inference. Fuzzy Syst 2009;FUZZ-IEEE 2009:80-5.
31. Yager RR, Filev DP. Generation of fuzzy rules by mountain clustering. J Intell Fuzzy Syst 1994;2:209-19.
32. Harding GW, Towe AL. An automated on-line, real-time laboratory for single neuron studies. Comput Biomed Res 1976;9:471-501.
33. The R Project for Statistical Computing. Available from: http://www.r-project.org/. [Last accessed on 21 Nov 2017].
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Zarei M. Spike discharge prediction based on neuro-fuzzy system. J Unexplored Med Data 2017;2:88-101. http://dx.doi.org/10.20517/2572-8180.2017.16
AMA Style
Zarei M. Spike discharge prediction based on neuro-fuzzy system. Journal of Unexplored Medical Data. 2017; 2: 88-101. http://dx.doi.org/10.20517/2572-8180.2017.16
Chicago/Turabian Style
Zarei, Mahdi. 2017. "Spike discharge prediction based on neuro-fuzzy system" Journal of Unexplored Medical Data. 2: 88-101. http://dx.doi.org/10.20517/2572-8180.2017.16
ACS Style
Zarei, M. Spike discharge prediction based on neuro-fuzzy system. J. Unexplored. Med. Data. 2017, 2, 88-101. http://dx.doi.org/10.20517/2572-8180.2017.16
About This Article
Copyright
Data & Comments
Data

 Cite This Article 0 clicks
Cite This Article 0 clicks











Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.